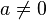Perbedaan eliminasi gauss dengan eliminasi Gauss-Jordan

Sejarah :

Salah satu metode yang dapat digunakan untuk menyelesaikan sistem persamaan linier adalah metode eliminasi Gauss-Jordan. Metode ini diberi nama Gauss-Jordan untuk menghormati "CarlFriedrich Gauss dan Wilhelm Jordan". Metode ini sebenarnya adalah modifikasi dari metode eliminasi Gauss, yang dijelaskan oleh Jordan di tahun 1887.

Penjelasan :

Metode Gauss-Jordan : menghasilkan matriks dengan bentuk baris eselon yang tereduksi 

(reduced row echelon form)

Eliminasi Gauss : hanya menghasilkan matriks sampai pada bentuk baris eselon

(row echelon form).

Metode Eliminasi Gauss adalah metode yang dikembangkan dari metode eliminasi, yaitu menghilangkan atau mengurangi jumlah variable sehingga dapat diperoleh nilai dari suatu variable yang bebas.

Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Metode Gauss Jordan ini digunakan untuk mencari invers dari sebuah matriks.

Prosedur umum  Gauss-Jordan : 

1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.

2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks

   A menjadi dalam bentuk baris eselon yang tereduksi

Pengubahan dilakukan dengan membuat matriks yang elemen-elemennya adalah koefisien-

koefisien dari sistem persamaan linier..

Sedangkan langkah-langkah pada operasi baris elementer yaitu :

1.Menukar posisi dari 2 baris.

Ai ↔Aj

2.Mengalikan baris dengan sebuah bilangan skalar positif.

Ai = k*Aj

3.Menambahkan baris dengan hasil kali skalar dengan baris lainnya

Algoritma Metode Eliminasi Gauss adalah:

1. Masukkan matrik A, dan vektor B beserta ukurannya n

2. Buat augmented matrik [A|B] namakan dengan A

3. Untuk baris ke i dimana i=1 s/d n, perhatikan apakah nilai ai,i =0 : Bila ya :

pertukarkan baris ke i dan baris ke i+k≤n, dimana ai+k ,i ≠0, bila tidak ada berarti perhitungan tidak bisa dilanjutkan dan proses dihentikan dengan tanpa penyelesaian. Bila tidak : lanjutkan

4. Untuk baris ke j, dimana j = i+1 s/d n

Flowchart :

Kelebihan dan Keuntungan :

Mengubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi. merupakan variasi dari eliminasi gauss dengan kebutuhan dapat menyelesaikan matriks invers.

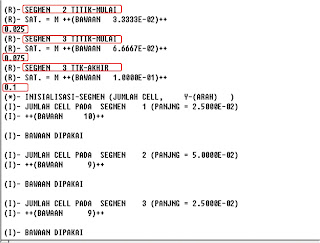
Contoh soal :

terima kasih semoga bermanfaat

Temperatur Pindah Panas (gravitasi)

continue

Aliran Fluida pada 2 pelat sejajar (variasi grid)

continue

Aplikasi Trapezoidal Simpson

continue..

Sifat Persamaan Akar - Akar Non Linear

Pada penjelasan ini saya hanya akan menjelaskan sifat - sifat persamaan akar non linear yang merupakan bagian dari metode iterative ( Persamaan akar Linear dan Non Linear) berikut penjelasan dari posting ini  :

• Metode Pengurung

Metode pengurung dimana nilai akar diperlukan penembakan nilai pertama dan kedua.

Keunggulan : Konvergensi (semakin banyak iterasi semakin mendekati nilai sebenarnya)

Kelemahan  : Konvergensi lambat

Contoh metode pengurung : 

1. Metoda Bisection (membagi dua) 
2. Metoda False Position (posisi palsu)

• Metode Terbuka

Metode terbuka yaitu metode mencari akar dimulai dari suatu nilai tunggal bebas dan tidak perlu dilakukan pengurungan.

Keunggulan : Konvergensi lebih cepat

Kelemahan  : Tidak selalu konvergen (kurang akurat)

Contoh metode terbuka :

1. Metode Newton Raphson
2. Metoda Secant (garis potong)
3. Metode Successive Aproximation 

*Untuk lebih memahami coba aj klik masing masing linknya

Terima Kasih Semoga Bermanfaat

Sifat Persamaan Akar Linear (Kuadratik Polinomial)

Pada posting kali ini saya akan mencoba berbagi ilmu yaitu penjelasan persamaan akar kuadrat. suatu persaamaan yang di kala SMA sering sekali digunakan, berikut penjelasan singkatnya..

Persamaan Kuadrat adalah suatu persamaan polinomial berorde dua. Dalam penjelasan ini  sesuai dengan matematika teknik dimana variabel akar persamaan sama dengan 0 dengan kata lain bersifat linear. Dengan bentuk umum yang sering dipelajari adalah bentuk kuadrat yaitu

Dimana :

x adalah variabel persamaan kuadrat

a adalah koefisien x kuadrat   

b adalah koefisien x

c adalah konstanta

Dengan 

Cara singkat mencari persamaan kuadrat :

• Metode mencari faktor :

• Metode memakai rus ABC :

• Metode Kuadrat Sempurna:

dumana q > 0

Jenis akar-akar persamaan kuadrat ditentukan oleh nilai deskriminan :

Mencari akar persamaan dapat melakukan metode langsung caranya dengan Rumus ABC :

Menggunakan cara cepat jika bentuk persamaannya sebagai berikut :

Sifat - sifat persamaan akar kuadrat :

Pengaplikasian dengan VB excel : klik disini

Terima Kasih semoga bermanfaat =D

CFD - Grid dependency Test

Pada posting ini catatan dilanjutkan dengan melakukan grid dependency test dengan kasus pada 2 pelat sejajar berikut saya tampilkan gambarannya : cekidot broww..

Pada soal berikut terdapat 2 pelat sejajar yang berjarak H = 0,1 m dengan Panjang L = 1m, kemudian pelat tersebut dialiri udara (laminer) dengan densitas r = 1.2 kg/m3. Dari gambaran tersebut terdapat 2 kasus yang harus diselesaikan dengan cara mengganti suatu parameter.

1. Mengganti viskositas m=4x10-5 kg/m.s dan m= 10-5 kg/m.s dengan menetapkan

kecepatan inlet uinlet=0,01m/s

2. Mengganti kecepatan inlet uinlet=0,01m/s dan uinlet=0,04m/s dengan menetapkan

viskositas m=4x10-5 kg/m.s

Langkah kerjanya :

1. Membuat 2 dimensi dengan ukuran panjang 1 m dan tinggi 0.1 m
2. Atur jumlah cell (50 x 30)
3. Pada kasus ini diberikan grid yang berbeda yaitu dengan penambah faktor pemberat dengan tujuan untuk lebih merapatkan cell guna memudahkan untuk melihat fenomena yang terjadi di daerah tersebut. apakah terjadi vortek apakan ada perubahan tekanan ddan kecepatan dan juga fenomena dasar aliran yang akan kita lihat.
4. Melakukan pembagian segmen pada arah x maupun arah y. segmen x dibagi menjadi 2 bagian (28 cell dan 20 cell). sumbu y dibagi menjadi 3 segmen (10 cell, 8 cell dan 10 cell).
5. Pada kasus 1 diberikan 2 inlet dengan perlakuan yang berbeda inlet 1 diberikan kecepatan udara 0.01 dan inlet 2 diberika tekanan 0 pa.

Berikut gambar simulasi CFDSOF :